矩陣是一個方形的數字陣列
將一些元素置換成若干行,每行放上相同數量的元素,就是一個矩陣。
從數學的定義上觀察,一個 m X n 的矩陣是一個由 m 列(Row)n 行(column)元素置換成的矩形陣列;矩陣裡的元素可以是數字、符號或數學式。

或展開為 1 列的矩陣 A = [ 1 , 2 , 3 , 4 ]

矩陣的一個重要用途是解線性方程組
線性方程組中未知量的係數可以排成一個矩陣,加上常數項,則稱為增廣矩陣。另一個重要用途是表示線性變換,即是諸如 f(x) = 2x 之類的線性函數的推廣。設定基底後,某個向量 v 可以表示為 m x 1 的矩陣,而線性變換 f 可以表示為行數為 m 的矩陣 A,使得經過變換後得到的向量 f(v) 可以表示成 Av 的形式。
矩陣的特徵值和特徵向量可以揭示線性變換的深層特性,是高等代數學中的常見工具,也常見於統計分析等應用數學學科中;在物理學中,矩陣於力學、電路學、光學和量子物理中都有應用;計算機科學中,三維動畫製作也需要用到矩陣。


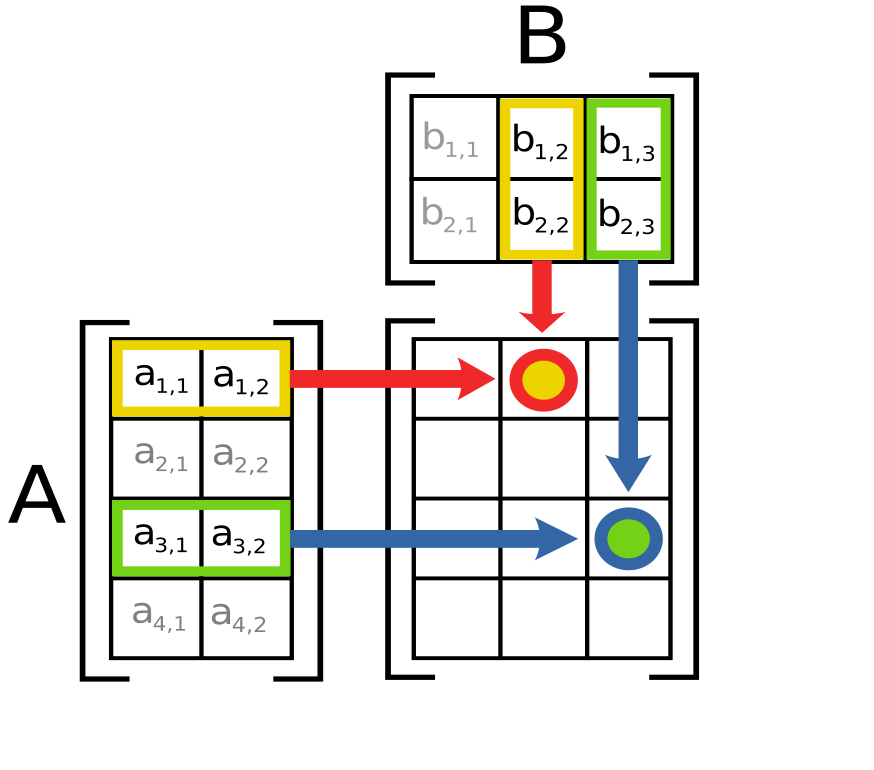
矩陣的運算是數值分析領域的重點
將矩陣分解為簡單矩陣的組合可以在理論和實際應用上簡化矩陣的運算。最基本運算包括:
- 矩陣加(減)法
- 純量乘法
- 轉置運算

